BATSWEB Home > Scienza e Cultura > Matematica del Bats > Geometria > Trigonometria

LA MATEMATICA DEL BATS

La trigonometria

La trigonometria č la parte della matematica che studia le funzioni circolari. Data una circonferenza di raggio unitario con il centro nell'origine e assumendo il senso antiorario come positivo, il punto P mobile sulla circonferenza individua un arco e un angolo corrispondente.

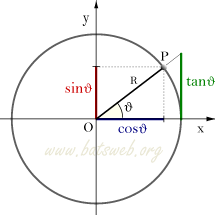
Il seno (sin) e il coseno (cos) dell'angolo θ sono due funzioni periodiche di periodo 2p definite come l'ordinata e l'ascissa del punto P. La tangente (tan) č definita come il rapporto sin θ / cos θ, ed č una funzione periodica di periodo p. Le altre funzioni trigonometriche sono la secante (sec θ = 1/cos θ) la cosecante (cosec θ = 1/sin θ) e la cotangente (cotan θ = 1/tan θ).

La relazione trigonometrica fondamentale č:

dalla quale derivano le seguenti relazioni trigonometriche:

sinē θ = tanē θ / ( 1 + tanē θ ) cosē θ = 1 / ( 1 + tanē θ ) tanē θ = sinē θ / ( 1 - sinē θ )
sinē θ = 1 - cosē θ cosē θ = 1 - sinē θ tanē θ = ( 1 - cosē θ ) / cosē θ
  

Valgono le seguenti relazioni:

sin (π/2 - α) = cos α cos (π/2 - α) = sin α
sin (π/2 + α) = cos α cos (π/2 + α) = - sin α
sin (π - α) = sin α cos (π - α) = - cos α
sin (π + α) = - sin α cos (π + α) = - cos α

Alcune formule notevoli:

formule di addizione: sin (α+β) = sin α cos β + sin β cos α
cos (α+ β) = cos α cos β - sin α sin β
tan (α+ β) = tan α tan β / ( 1 - tan α tan β )
formule di duplicazione:  sin (2α) = 2 sin α cos α
cos (2α) = cosē α - sinē α = 2 cosē α - 1
tan (2α) = tanē α / ( 1 - tanē α )
formule di prostaferesi:  sin α + sin β = 2 sin [(α+β)/2] cos [(α-β)/2]
sin α - sin β = 2 sin [(α-β)/2] cos [(α+β)/2]
cos α + cos β = 2 cos [(α+β)/2] cos [(α-β)/2]
cos α - cos β = -2 sin [(α+β)/2] sin [(α-β)/2]
formule di bisezione: sinē (α/2) = (1 - cos α)/2
cosē (α/2) = (1 + cos α)/2

Relazioni tra lati e angoli di un triangolo

Dato un triangolo qualunque di lati a,b,c e angoli opposti corrispondenti α, β,γ valgono le seguenti formule:

teorema dei seni: a / sin α = b / sin β = c / sin γ
teorema di Carnot: aē = bē + cē - 2 b c cos α
  

Dato un triangolo rettangolo valgono le seguenti relazioni:

b = h sin β
b = h cos γ
b = c tan β

< La geometria >
Torna ad inizio Pagina LA FISICA DEL BATS Ritorna alla Home Page