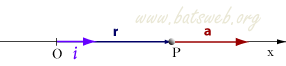
BATSWEB Home > Scienza e Cultura > Fisica del Bats > Meccanica > Cinematica > Moto uniformemente accelerato
Il moto di un punto P č uniformemente accelerato se sono costanti l'accelerazione e la sua componente tangenziale; in questo caso la velocitą varia linearmente e la traiettoria dipende dalla componente normale dell'accelerazione.
Nel moto rettilineo uniformemente accelerato l'accelerazione a = dv/dt č costante e la sua componente normale č nulla, quindi la traiettoria č rettilinea e la velocitą v varia linearmente.
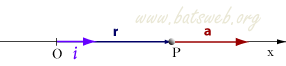
Dopo avere scelto un opportuno sistema di riferimento tale che a = a i, se all'istante t=0 la particella ha velocitą v(0) = v0 i e posizione r(0) = s0 i, la velocitą e la posizione all'istante t sono dati da:
![]()
![]()
Tabella delle relazioni che intercorrono tra il tempo e le grandezze cinematiche lineari (tempo, spazio, velocitą e accelerazione) in un moto uniformemente accelerato date le condizioni iniziali v=v0 e s=s0 per t = 0:
| grandezze conosciute | grandezze incognite | |
|---|---|---|
| t s | v = [ 2 ( s - s0 ) / t ] - v0 | a = 2 ( s - s0 - v0 t ) / t² |
| t v | s = s0 + ( v0 + v ) t / 2 | a = ( v - v0 ) / t |
| t a | s = s0 + v0 t + ½ a t² | v = v0 + a t |
| s v | t = 2 ( s - s0 ) / ( v + v0 ) | a = ( v² - v0² ) / [ 2 ( s - s0 ) ] |
| s a | t = { - v0 ± √ [ v0² + 2 a ( s - s0 ) ] } / a | v = ± √ [ v0² + 2 a ( s - s0 ) ] |
| v a | t = ( v - v0 ) / a | s = s0 + ( v² - v0² ) / 2 a |
Nel moto circolare uniformemente accelerato le componenti tangenziale e normale dell'accelerazione lineare a = dv/dt sono entrambi costanti: la traiettoria č una circonferenza e la velocitą lineare v varia linearmente. Dato che la componente tangenziale di a č costante, anche l'accelerazione angolare α č costante. di conseguenza la velocitą angolare ω varia linearmente.
|
Se il raggio e la velocitą giacciono sul piano individuato da i e j, e se all'istante t=0 la particella ha velocitą angolare ω(0) = ω0 e posizione angolare θ(0) = θ0, la velocitą e la posizione angolare all'istante t sono dati da:
|
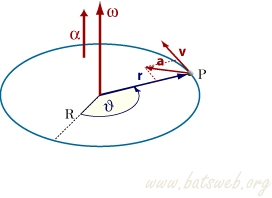 |
Tabella delle relazioni che intercorrono tra il tempo e grandezze cinematiche angolari (tempo, angolo, velocitą angolare e accelerazione angolare) in un moto uniformemente accelerato date le condizioni iniziali ω=ω0 e θ=θ0 per t = 0:
| grandezze conosciute | grandezze incognite | |
|---|---|---|
| t θ | ω = [ 2 ( θ - θ0 ) / t ] - ω0 | α = 2 ( θ - θ0 - ω0 t ) / t² |
| t ω | θ = θ0 + ( ω0 + ω ) t / 2 | α = ( ω - ω0 ) / t |
| t α | θ = θ0 + ω0 t + ½ α t² | ω = ω0 + α t |
| θ ω | t = 2 ( θ - θ0 ) / ( v + v0 ) | α = ( ω² - ω0² ) / [ 2 ( θ - θ0 ) ] |
| θ α | t = { - v0 ± √ [ v0² + 2 α ( θ - θ0 ) ] } / α | ω² = ω0² + 2 α ( θ - θ0 ) |
| ω α | t = ( ω - ω0 ) / α | s = s0 + ( ω² - ω0² ) / 2 α |
< La cinematica >
| Torna ad inizio Pagina | LA FISICA DEL BATS | Ritorna alla Home Page |