BATSWEB Home >
Scienza e Cultura >
Fisica del Bats >
Meccanica >
Cinematica >
Vettore posizione
LA FISICA DEL BATS
Il vettore posizione
Per descrivere la posizione di una particella che si muove lungo una
curva occorre specificare un sistema di riferimento (che può essere qualunque) rispetto al quale il moto
viene misurato. La posizione di un punto al
variare del tempo t è individuata da un vettore
r(t) uscente dall'origine del sistema
di coordinate
prescelto. Il vettore può variare nel tempo in modulo e orientamento
percorrendo una traiettoria e la legge oraria viene espressa da un insieme di
equazioni parametriche in funzione del tempo.
r = r(t)
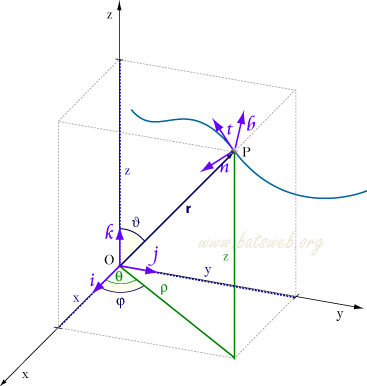
Vettore posizione nello spazio a tre dimensioni
Dato un sistema di riferimento Oxyz, individuato dai
versori i, j e k, rispetto alle coordinate del
punto P nello spazio il vettore posizione r di P è dato da:
| sistema
|
vettore posizione di P
|
| Coord. cartesiane (x,y,z)
|
r(t) = x i +
y j + z k
|
| Coord. cilindriche (ρ,θ,z)
|
r(t) = ρ cos θ
i + ρ sin θ j + z k
|
| Coord. polari (r,θ,φ)
|
r(t) = r cos φ sin θ
i + r sin φ sin θ j + r cos
θ k
|
Il modulo del vettore posizione
è dato da:
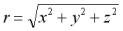
Rispetto al punto P è possibile definire nello spazio un
sistema di coordinate ortogonali mobile definito da t (versore
tangente), n (versore normale) e b (versore
binormale); se s è la lunghezza dell'arco percorso lungo la curva C e R è il
raggio di curvatura della curva valgono le formule:
| t = dr/ds
|
n = R · dt/ds
|
b =
t ^ n
|
|
|
 |
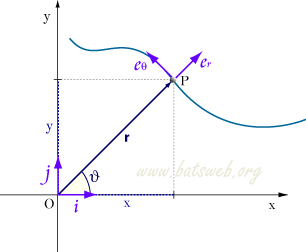
Vettore posizione nel piano
Dato un sistema di riferimento Oxy, individuato dai
versori i e j, rispetto alle coordinate del
punto P nel piano il vettore posizione r di P è dato da:
| sistema
|
vettore posizione di P
|
| Coordinate cartesiane (x,y)
|
r(t) = x i +
y j
|
| Coordinate polari (r,θ)
|
r(t) = r cos θ
i + r sin θ j
|
Il modulo del vettore posizione
è dato da:
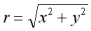
E' possibile trovare le componenti del vettore posizione di P rispetto ai
versori er, eθ,
che
individuano rispettivamente la direzione di r e la direzione perpendicolare a r
nella direzione positiva di θ. Valgono le seguenti relazioni di
trasformazione:
er = cos
θ i
+ sin θ j
eθ = - sin θ i
+ cos θ j
|
i = cos θ er
- sin θ eθ
j = sin θ er
+ cos θ eθ
|
In questo caso il vettore posizione è dato da:
r (t) = r ( cos θ
i + sin θ j ) = r er
|
|
 |
< La cinematica
>
![]()

