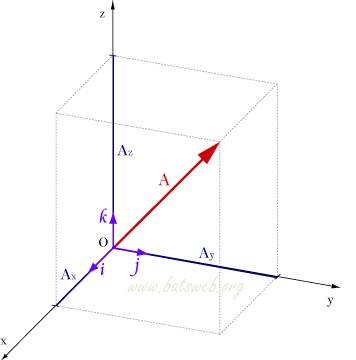
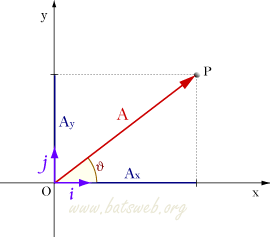
Se il punto terminale di un vettore A uscente dall'origine è un punto di coordinate (A_x,A_y,A_z), queste coordinate sono dette componenti del vettore, ed è possibile rappresentare ogni vettore nei termini delle sue componenti:

Il modulo di un vettore è uno scalare non negativo definito da:

Dati i punti P₁(x₁,y₁,z₁) e P₂(x₂,y₂,z₂), il vettore che li congiunge è dato da: PQ = (x₂-x₁) i + (y₂-y₁) j + (y₂-y₁) k. Se A = A_x i + A_y j + A_z k = A ( l i + m j + n k ), le componenti:

l = cos α,  m= cos β,  n = cos γ

del versore che individua la direzione di A sono dette coseni direttori. Dati i vettori A₁= A₂ l'angolo compreso tra di essi è dato da:

φ = arc cos ( l₁ l₂+ m₁ m₂+ n₁ n₂ )

Nel piano la coppia di versori ortogonali i, j individua un sistema di riferimento. Se il punto terminale di un vettore A uscente dall'origine è un punto di coordinate (A_x,A_y), il vettore e il suo modulo rispetto delle componenti sono rappresentati da:

Valgono le relazioni: