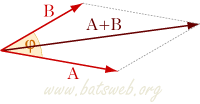
Dati i vettori A e B il vettore somma è un vettore A + B ottenuto traslando il secondo vettore in modo che l'origine di B coincida con il punto terminale di A e congiungendo l'origine di A con il termine di B (legge del parallelogrammo)

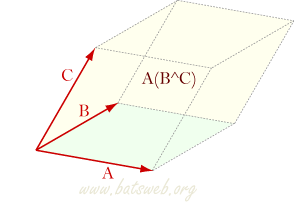
• valgono le proprietà commutativa e associativa: A+B = B+A ; A+(B+C) = (A+B)+C
• in termini di componenti: A + B = (A_x+B_x) i + (A_y+B_y) j + (A_z+B_z) k
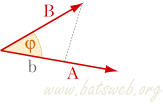
• dati i moduli A B e l'angolo φ compreso tra i vettori, il modulo R del vettore risultante è dato da: R² = A² + B² + 2AB cos φ
• la differenza A - B equivale alla somma di A con l'opposto di B

Il prodotto scalare (interno) di due vettori A e B è lo scalare A · B = A B cos φ (dove φ è l'angolo tra i due vettori compreso tra 0 e 2p).

• valgono le proprietà commutativa e distributiva: A·B = B·A ; A·(B+C) = (A+B)·C
• in termini di componenti: A · B = A_xB_x + A_yB_y + A_zB_z ; A · A = A_x² + A_y² + A_z² = A²
• la quantità scalare b = B cos φ è detta componente di B secondo A, e vale A · B = A b
• se A e B sono nulli o perpendicolari vale A · B = 0; quindi: i · j = j · k = i · k = 0
• valgono le relazioni: i · i = j · j = k · k = 1

Il prodotto vettoriale (esterno) di due vettori A e B è un vettore A ^ B di modulo A B sin φ (dove φ è l'angolo tra i due vettori compreso tra 0 e 2p), perpendicolare ai vettori dati (l'orientamento è tale che A , B e C formano un sistema destrorso).

• valgono le proprietà anticommutativa e distributiva: A^B = -B^A : A^ (B+C) = (A^B)+(A^C)
• in termini di componenti:
  

  A ^ B =	i	j	k	= ( AyBz - AzBy) i + ( AzBx - AxBz) i + ( AxBy - AyBx) k
  	Ax	Ay	Az
  	Bx	By	Bz

• la quantità scalare B_⊥ = B sin φ è detta componente di B nella direzione perpendicolare ad A, e vale | A ^ B | = A B_⊥
• se A e B sono paralleli e non sono entrambi nulli vale A ^ B = 0; quindi i ^ i = j ^  j = k ^ k = 0
• valgono le relazioni: i ^ j = k ;  j ^ k = i; k ^ i = j
• in geometria | A ^ B | è l'area del parallelogrammo delimitato da A e B

Il prodotto triplo di tre vettori A, B e C è lo scalare A · ( B ^ C )

• in termini di componenti:
  

  A · ( B ^ C ) =	Ax	Ay	Az	= Ax ( ByCz - BzCy) + Ay ( BzCx - BxCz) + Az ( BxCy - ByCx)
  	Bx	By	Bz
  	Cx	Cy	Cz

• in geometria A · ( B ^ C ) è il volume del parallelogrammo delimitato da A, B e C