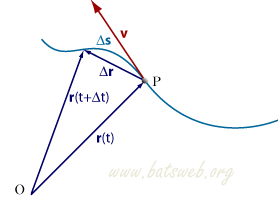
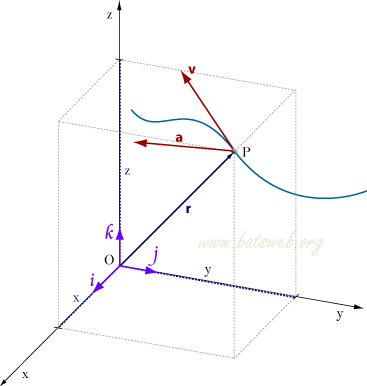
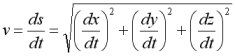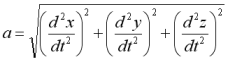Lo spazio percorso da un punto materiale in un intervallo di tempo è misurato con il vettore spostamento, diverso dall'arco di curva Δs percorso nel medesimo intervallo:
Δr = r (t+Δt) - r(t)
Per calcolare la velocità istantanea di un corpo, che misura la rapidità di variazione del vettore posizione, si considera il rapporto tra lo spostamento Δr e l'intervallo di tempo Δt impiegato a percorrerlo (velocità media) e si fa tendere questo intervallo a zero: questa idea portò al concetto matematico di derivata, una delle basi del calcolo differenziale. Quindi il vettore velocità di una particella in qualsiasi istante è la derivata prima del vettore posizione rispetto al tempo:
![]()
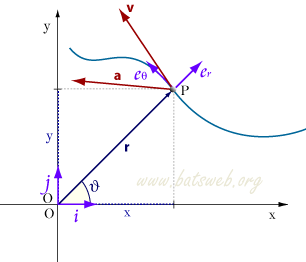
Se s è la lunghezza dell'arco percorso lungo la curva C, il modulo della velocità (velocità scalare) è dato da:
v = |v| = ds/dt
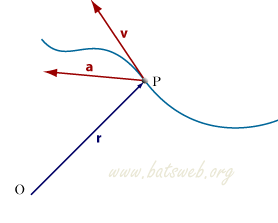
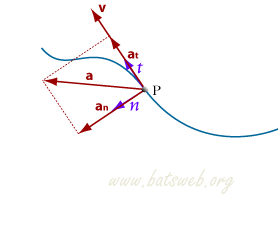
Il vettore accelerazione (che misura la rapidità di variazione della velocità) è la derivata derivata prima della velocità rispetto al tempo, quindi è la derivata seconda del vettore posizione:
![]()