BATSWEB Home > Scienza e Cultura > Fisica del Bats > Meccanica > Cinematica > Moto dei proiettili

LA FISICA DEL BATS

Il moto di un proiettile

Supponendo che la Terra sia un sistema di riferimento inerziale e che non ci sia resistenza dell'aria, il moto di un proiettile č la combinazione di un moto verticale accelerato dovuto alla gravitą e un moto orizzontale uniforme dovuto all'inerzia che non interferiscono tra loro.

Dato un sistema di riferimento Oxyz, se le condizioni iniziali per t=0 sono r(0) = 0, v(0) = vx i + vz k allora per il principio di inerzia (moto rettilineo uniforme) vale x(t) = vx t e per la legge di caduta dei gravi (moto rettilineo uniformemente accelerato) vale: z(t) = zy t - ½ g t². Quindi le equazioni del moto del proiettile sono le seguenti:

r(t) = ( vx t ) i + ( vz t - ½ g t² ) k
v(t) = dr/dt = vx   j + ( vz - g t ) k
a(t) = dv/dt = - g  k

 

    

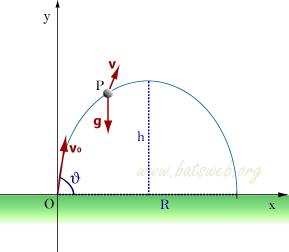Se v0 č il modulo della velocitą iniziale e θ č l'angolo di tiro rispetto all'asse x, valgono le seguenti relazioni:

velocitą iniziale vo = √[ vx² + vz² ]  vx =  vo cos θ
 vy =  vo sin θ
angolo di tiro θ = arc tan ( vz / vx )  θ = ½ arc sin ( g R / vo)
traiettoria del proiettile z = ( vz / vx ) x - [ g  / ( 2 vx² ) ] x² z = ( tan θ ) x - [ g  / ( 2 vo² cos² θ ) ] x²
quota del vertice della traiettoria hV = vz² / 2 g hV = v0² sin² θ / 2 g
gittata  R = 2 vx vz / g R = v0² sin (2 θ) / g
tempo di volo t = 2 vz / g t = 2 v0 sin θ / g

< La cinematica >
Torna ad inizio Pagina LA FISICA DEL BATS Ritorna alla Home Page